Un enfoque práctico de la metaheurística al usar LabVIEW y MATLAB

A practical approach to Metaheuristics using Labview and Matlab
Dr. David Christopher Balderas Silva
dc.balderassilva@tec.mx

Un problema de optimización es el encontrar la mejor solución entre todas las soluciones factibles. En matemáticas, para ciertos problemas, esta solución se puede encontrar por medio del uso de métodos exactos. La dificultad radica en que muchos problemas son NP-completos, una clase de problemas de decisión los cuales requieren de amplio gasto computacional para resolverlos. No se conoce una forma eficiente de encontrar una solución rápida y precisa para estos problemas, aunque las soluciones pueden verificarse cuando se dan. Como alternativa los métodos de optimización se aplican en varios campos[1]. Los métodos de optimización tradicionales están enfocados en técnicas basadas en derivadas. Sin embargo, esas técnicas frecuentemente se quedan atrapadas en mínimos locales y se limitan a ser apropiadas para funciones de optimización muy específicas.

Hay dos condiciones fundamentales cuando se realiza una búsqueda de optimización: exploración y explotación[2]. La exploración busca la solución en regiones completamente nuevas del espacio de búsqueda, por otro lado la explotación busca en regiones del espacio de búsqueda dentro de los puntos previamente visitados (ver Figura 01). Como resultado, un algoritmo de optimización requiere implementar un compromiso entre exploración y explotación. En consecuencia, se han desarrollado metodologías de optimización heurística con el fin de tratar problemas que los métodos derivativos no son capaces de resolver [1]. Un algoritmo heurístico es aquel que está diseñado para resolver un problema de una manera más rápida y eficiente que los métodos tradicionales sacrificando la optimización, la precisión, o la integridad por la velocidad.  La heurística puede producir una solución individualmente o usarse para proporcionar una buena línea de base y se complementa con los algoritmos de optimización. Los algoritmos heurísticos se emplean cuando las soluciones aproximadas son suficientes y las soluciones exactas son necesariamente costosas computacionalmente.

Más a detalle, la optimización heurística es una metodología que intenta lograr una solución buena y factible mediante una evaluación que sigue ciertas reglas(o heurísticas) las cuales parecen atractivas para encontrar una solución. Esta solución generalmente tiene que encontrarse en un corto período de tiempo y es muy útil cuando no se pueden evaluar todas las soluciones o combinaciones en un espacio de búsqueda. Cabe recalcar que con frecuencia no se alcanza la mejor solución. Los algoritmos metaheurísticos utilizan la aleatorización de compensación y una búsqueda local para tratar de encontrar una mejor global.

Probablemente, la primera aplicación de un algoritmo heurístico fue revelada en la Segunda Guerra Mundial por Alan Turing, quien desarrolló un algoritmo para descifrar mensajes alemanes. El algoritmo pudo encontrar la combinación correcta en un tiempo razonablemente práctico. Turing llamó búsqueda heurística a este algoritmo [3].

Se podría hacer una clasificación general de algoritmos metaheurísticos inspirados utilizando cinco conjuntos: métodos basados en la evolución, métodos basados en la física, métodos basados en enjambres, métodos basados en humanos y métodos basados en fenómenos naturales[4]. El recocido simulado es uno de los algoritmos metaheurísticos más representativos, fue propuesto por Scott Kirkpatrick, C. Daniel Gelatt y Mario P. Vecchi en 1983 [5]; este algoritmo se inspiró en el proceso de recocido de metales. El método permite salir de los óptimos locales y podría incluir un factor de probabilidad. En 1960 John Holland introdujo los algoritmos genéticos basados en el concepto de evolución de la teoría de Darwin, los cuales fueron extendidos por su alumno David E. Goldberg en 1989 [6]. Más tarde, en 1986, Fred Glover presentó una metodología llamada Tabu Search y poco después en 1992 se desarrolló Ant Colony; estos algoritmos se volvieron ampliamente conocidos, pero en 1995 J. Kenedy y Russell crearon una de las metodologías más importantes de optimización metaheurística llamada Particle Swarm Optimization (PSO) [10]. La inteligencia de enjambres de pájaros y peces fue la inspiración de esta metodología que permite resolver complejos problemas de optimización [2]. Se demostró que PSO es mejor que los algoritmos de búsqueda tradicionales y en ciertos casos incluso mejor que los algoritmos genéticos [2]. En 2017 se propuso una nueva propuesta llamada optimización de terremotos, inspirada en la naturaleza de los terremotos [7]. Observando la naturaleza, es una excelente alternativa para crear nuevos métodos de optimización, en este caso, el terremoto de la Ciudad de México que devastó toda la ciudad sirvió para proponer un algoritmo que se basó en este fenómeno físico.

Como se ve, hay varios algoritmos metaheurísticos que han sido implementados exitosamente. Sin embargo, algunos desafíos que deben abordarse, como la precisión cuando se trata de conjuntos de datos incompletos, es un desafío que aún no se ha resuelto por completo. Por ejemplo, la precisión de la clasificación está relacionada con el método del algoritmo de aprendizaje. Por lo tanto, el mismo conjunto de datos aplicado a diferentes algoritmos de clasificación lograron  precisiones diferentes. Así mismo existen otros desafíos como la estabilidad, la escalabilidad y el costo computacional [8]. Por otro lado, cuando DH Wolpert y Macready publicaron los teoremas de optimización se mostró que no existe un algoritmo universal mejor para todos los problemas, por lo que la idea de crear un algoritmo para todos los problemas no es válido; es mejor crear un algoritmo para la mayoría de los diversos tipos de problemas [9]. Por ejemplo, el algoritmo A funcionara mejor que el algoritmo B para una funciones, entonces B superará a A en otras funciones.

Cuando buscamos propiedades esenciales en algoritmos de optimización, comúnmente se evalúan la robustez, eficiencia y precisión. La robustez permite encontrar buenas soluciones a una variedad de problemas de la misma clase, la eficiencia restringe los recursos computacionales como el tiempo computacional y / o el almacenamiento, finalmente, la precisión intenta evitar ser extremadamente sensible a errores en los datos o errores de cálculo causados ​​por redondeo de cálculos cuando se utiliza un cálculo digital. Sin embargo, en general, estas características están en conflicto unos a otros [11].

De hecho, los algoritmos permiten combinar con varias técnicas y pueden implementarse en línea utilizando hardware especializado como FPGAs. Además, el desarrollo de computadoras permite crear novedosas metodologías de optimización. Actualmente, los algoritmos de optimización se pueden utilizar para resolver varios problemas de optimización complejos. Esta complejidad se determina de acuerdo con la naturaleza real y práctica de la función objetivo o las restricciones del modelo.

Dentro de  los entornos de programación sobresalen dos lenguajes los cuales tienen amplia usabilidad en la ciencia y en la ingeniería: LabVIEW y MATLAB. National Instrument es una empresa que desarrolla hardware y software que permite generar productos académicos e industriales . Uno de los mejores software industrial y académico desarrollado por National Instruments para crear software que se puede conectar con hardware se llama LabVIEW [13]. Este software se puede conectar directamente con hardware como DAQ, My DAQ, CompactRIO, etc. Este equipo podría ser utilizado por la academia y la industria para proponer, probar y validar nuevas metodologías, así como para diseñar prototipos rápidos y trasladarlos a un producto final utilizando el mismo software y hardware.

MATLAB es un software orientado a la realización de proyectos matemáticos que incluyen cálculos complejos o de gran magnitud y permite su visualización [12]. MATLAB es una contracción de Matrix Laboratory, dado que se desarrolló inicialmente para manejar matrices para álgebra lineal. En estos días, MATLAB se utiliza en un gran número de universidades, ya que es una herramienta útil para impartir cursos como álgebra lineal, procesamiento de imágenes, ecuaciones diferenciales, análisis complejo, teoría de control, inteligencia artificial, etc. Además, en la actualidad, es uno de los software más utilizado para la ciencia, ya que tiene altas capacidades matemáticas, muchos paquetes, muchas implementaciones desarrolladas por el usuario, interacción con varios tipos de software y hardware, y capacidades de modelado. Dentro de MATLAB se encuentra Simulink [14] el cual es un entorno gráfico para la simulación basado en modelos de sistemas dinámicos. Algunas de las principales ventajas de Simulink es la capacidad de modelar sistemas no lineales, donde la función de transferencia puede no ser fácilmente solucionable y poder incorporar las condiciones iniciales al sistema.

Sobre estos temas se desarrolló un libro el cual es un compendio del uso de optimización metaheurística dentro de los dos populares softwares como lo son Labview y Matlab Figura 02. Dentro del libro se pueden ver varios métodos de optimización los cuales cuentan con ejemplos. Los métodos seleccionados fueron Nelder-Mead, Genetic Algorithm, Simulated Annealing, Particle Swarm Optimization, Bat Optimization, Gray Wolf Optimization, Earthquake Optimization, Tabu search, and Ant Colony Optimization.

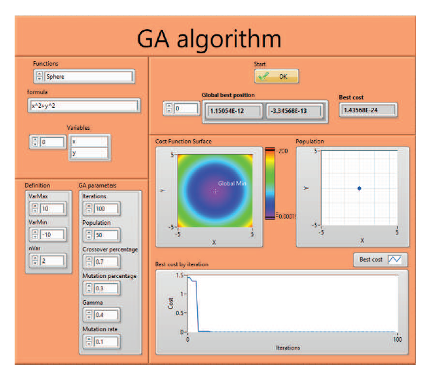
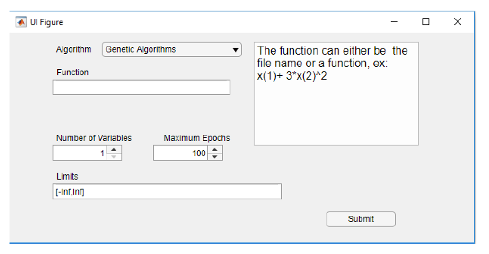
Asimismo, como parte del libro, se crearon un toolkit y una APP las cuales permiten introducir diversas funciones las cuales se pueden optimizar con cualquiera de los métodos descritos. Tanto el toolkit como la APP cuentan con varios botones donde se pueden seleccionar cada una de las técnicas explicadas dentro del libro, y se pueden  manejar los diversos hiperparametros de cada una de las técnicas de optimización con solo un click (ver Figura 04).

1. Mohammed R AlRashidi and Mohamed E El-Hawary. A survey of particle swarm optimization applications in electric power systems. IEEE transactions on evolutionary computation, 13(4):913{918, 2008.
2. Matej Crepinsek, Shih-Hsi Liu, and Marjan Mernik. Exploration and exploitation in evolutionary algorithms: A survey. ACM Computing Surveys (CSUR), 45(3):35, 2013.
3. Xin-She Yang. Nature-inspired metaheuristic algorithms. Luniver press, 201
4. R Rajakumar, P Dhavachelvan, and T Vengattaraman. A survey on nature inspired meta-heuristic algorithms with its domain specifications. In 2016 International Conference on Communication and Electronics Systems (ICCES), pages 1{6. IEEE, 2016.
5. Peter JM Van Laarhoven and Emile HL Aarts. Simulated annealing. In Simulated annealing: Theory and applications, pages 7-15. Springer, 1987.
6. Holland, John H. «Genetic algorithms.» Scientific american 267.1 (1992): 66-73.
7. Ponce Pedro and Molina Arturo. Earthquake optimization algorithm, internal report binational laboratory project, 2017.
8. Wei Liu and Jianyu Wang. A brief survey on nature-inspired metaheuristics for feature selection in classification in this decade. In 2019 IEEE 16th International Conference on Networking, Sensing and Control (ICNSC), pages 424{429. IEEE, 2019.
9. Wolpert, David H., and William G. Macready. «No free lunch theorems for optimization.» IEEE transactions on evolutionary computation 1.1 (1997): 67-82.
10. Kennedy, J.; Eberhart, R. (1995). «Particle Swarm Optimization». Proceedings of IEEE International Conference on Neural Networks. IV. pp. 1942–1948.
11. Jorge Nocedal and Stephen Wright. Numerical optimization. Springer Science & Business Media, 2006.
12. Chapra, Steven C. Applied numerical methods with MATLAB for engineers and scientists. New York: McGraw-Hill,, 2012.
13. Blume, Peter A. LabVIEW Style Book, The (Paperback). Pearson Education, 2007.
14. Messner, William C., Dawn M. Tilbury, and Rick Hill. «Control tutorials for matlab® and simulink®.» (1999).